چطور بینهایتها را اندازهگیری میکنند!
برای پاسخ به سؤالات مربوط به درک اندازهی مجموعههای بینهایت، اجازه دهید کار را با مجموعههایی از اعداد شروع کنیم که شمارش آنها آسانتر است. مجموعهای از اشیاء، اعداد یا عناصر که شامل تعداد محدودی از این المانها است را در نظر بگیرید.
در اینجا ما دو نمونه از مجموعههای چهار عضوی و متناهی را در نظر میگیرم.
همانطور که میبینید تعیین اندازهی یک مجموعهی متناهی آسان است، چراکه تنها کافیست تعداد عناصر موجود در آن را بشمارید. از آنجایی که مجموعه متناهی است، میدانید که در نهایت شمارش متوقف خواهید شد و شما اندازهی مجموعه را به دست خواهید آورد. در عین حال کاملا مشخص است که این استراتژی برای مجموعههای بینهایت کارآمد نیست. بنابراین رویه را به شکل دیگری پیش میگیریم. در اینجا مجموعهای از اعداد طبیعی که با ℕ نشان داده میشود را در نظر میگیریم. البته ممکن است استدلال کنید که صفر یک عدد طبیعی نیست، اما این بحث بر تحقیقات ما در مورد بینهایتها تاثیرگذار نیست.
ℕ={۰،۱،۲،۳،۴،۵،…}
اندازهی این مجموعه چقدر است؟
از آنجایی که بزرگترین عدد طبیعی وجود ندارد، تلاش شما برای شمارش تعداد عناصر این مجموعه بیمعنی است. در همین راستا یک راه حل این است که به سادگی اندازهی این مجموعهی نامتناهی را بینهایت اعلام کنید که اشتباه هم نیست، اما زمانی که با مجموعههای نامتناهی بیشتر سروکله بزنید، متوجه میشوید که این حرف چندان هم درست نیست!
مجموعهای از اعداد حقیقی را در نظر بگیرید که همهی اعداد آن قابل بیان در یک بسط اعشاری ۸.۰۱۵- ,۳.۲ ,۷ یا یک بسط بینهایت مانند …۱.۴۱۴۲۱۳=۲–√ باشند. از آنجایی که هر عدد طبیعی یک عدد حقیقی هم است، میتوان بیان کرد که مجموعهی اعداد حقیقی حداقل به اندازهی مجموعهی اعداد طبیعی است، بنابراین باید بینهایت هم باشد. اما بیان اندازهی بینهایت مجموعهی اعداد حقیقی هم به همان اندازه غیر قابل قبول است. به منظور درک این موضوع دو عدد مانند ۳ و ۷ را انتخاب میکنیم. طبیعی است که بین این دو عدد تعداد متناهی از اعداد طبیعی مانند ۶ ,۵ ,۴ وجود دارد اما اعداد حقیقی بین این دو عدد، بینهایت ( π ,۴.۰۱۰۲۳ ,۵.۶۶۶ و غیره) است.
بنابراین مهم نیست دو عدد حقیقی مجزا چقدر به یکدیگر نزدیک باشند، همیشه تعداد بینهایت اعداد حقیقی در بین آنها وجود خواهد داشت. البته باید بدانید که این موضوع به خودی خود به این معنی نیست که مجموعهئ اعداد حقیقی و اعداد طبیعی اندازههای متفاوتی دارند، اما نشان می دهد که اساساً چیزی متفاوت در مورد این دو مجموعهی نامتناهی وجود دارد که مستلزم بررسی بیشتر است! در همین راستا گئورگ کانتور «Georg Cantor» در اواخر قرن نوزدهم این موضوع را بررسی کرد. او نشان داد که این دو مجموعهی بینهایت به معنی واقعی اندازهی متفاوتی دارند. برای چگونگی درک این مطلب، ابتدا باید نحوهی مقایسهی مجموعههای بینهایت را یاد بگیرید که با کمک توابع ممکن خواهد بود.
راههای مختلفی برای درک توابع وجود دارد که شامل نمادگذاری تابعی مانند f(x)=x+1، نمودارهای سهمی در صفحهی دکارتی، دستوراتی مانند ورودی را بگیرید و ۳ را به آن اضافه کنید و غیره میشود. ما در این قسمت از یک تابع برای تطبیق عناصر یک مجموعه به عناصر مجموعهی دیگر استفاده میکنیم. با توجه به همین مساله برای مجموعهی اول اعداد طبیعی (ℕ) را در نظر میگیریم برای مجموعهی دیگر، که ما آن را S مینامیم، همهی اعداد طبیعی زوج را انتخاب میکنیم.
N={0,1,2,3,4,…} S={0,2,4,6,8,…}
تابع سادهی f(x)=2x عناصر ℕ را به عناصر S تبدیل میکند. به این معنی که این تابع ورودیهای خود را دو برابر میکند، بنابراین اگر عناصر ℕ را به عنوان ورودی f(x) در نظر بگیریم (مجموعه ورودی های یک تابع را دامنهی آن مینامیم!)، خروجیها همواره عناصر S خواهند بود. به عنوان مثال f(0)=0, f(3)=6 و غیره! میتوانید این کار را با ردیف کردن عناصر دو مجموعه در کنار هم انجام دهید و سپس با استفاده از فلشها نشان دهید که چگونه تابع f ورودیها را از ℕ به خروجی در S تبدیل میکند.
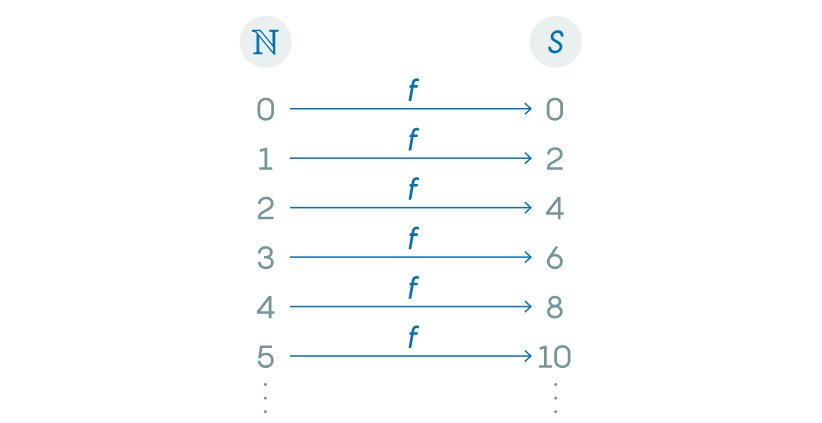
توجه کنید که چگونه f(x) دقیقاً یک عنصر از S را به هر عنصر در ℕ اختصاص میدهد. ابتدا f همهی عناصر را در S به ℕ اختصاص میدهد به زبان فنیتر هر عنصر S، تصویر یک عنصر ℕ در تابع f است، مثلا عدد زوج ۳۴۷۲ در S به شکل f(x)=3472 نوشته میشود و نظیر ℕ آن عدد ۱۷۳۶ است. به عبارتی تابع f(x) اعداد ℕ را روی S نگاشت «maps» میکند. به طور کلی اولین نکتهی مهم در تبدیل عناصر دو مجموعه به یکدیگر این است که تابع f(x) (یک تابع پوشا «surjective») ورودیها را از مجموعهی ℕ به خروجیای در S تبدیل میکند و هیچ چیزی در مجموعهی S از دست نمیرود.
دومین نکته ویژه در مورد نحوهی اختصاص دادن خروجیهای f(x) به ورودیها این است که هیچ دو عنصری در ℕ به یک عنصر در S تبدیل نمیشوند. به این معنی که اگر دو عدد در ℕ متفاوت باشند دو برابر آنها هم متفاوت خواهد بود. در چنین حالتی میگوییم که تابع ما یک به یک «injective» (۱-۱ هم نوشته میشود!) است. بنابراین تاکید میکنیم که هر عنصر در S تنها با یک عنصر در ℕ جفت میشود.
این دو ویژگی تابع f(x) به شکلی قدرتمند با هم ترکیب میشوند، به این معنی که تابع f(x) تطابق کاملی بین عناصر ℕ و عناصر S ایجاد میکند! این واقعیت که f(x) تابعی پوشا است به این معنی است که هر چیزی در S شریکی در ℕ دارد و این واقعیت که تابع ۱ به ۱ است به این معنی است که هیچ چیز در S به دو شریک در ℕ تبدیل نمیشود. به طور خلاصه، تابع f(x) هر عنصر ℕ را دقیقا با یک عنصر S جفت میکند.
توابعی که هم پوشا و هم یک به یک باشند، توابع یک به یک و پوشا «bijection» نامیده میشوند و از آنجایی که چنین تابعی همراه با این دو ویژگی یک مطابقت ۱ به ۱ بین این دو مجموعه ایجاد میکنند به این معناست که هر عنصر در یک مجموعه دقیقاً یک شریک در مجموعهی دیگر دارد و این یکی از راههای نشان دادن اندازهی یکسان دو مجموعهی بینهایت است.
از آنجایی که هر عنصر در یک مجموعه دقیقاً یک شریک در مجموعهی دیگر دارد یکی از راههای نشان دادن اندازهی یکسان دو مجموعهی بینهایت است.
توابع یک به یک و پوشا یک مطابقت ۱ به ۱ بین دو مجموعه ایجاد میکنند که به این معناست که هر عنصر در یک مجموعه دقیقاً یک شریک در مجموعه دیگر دارد. چنین روشی، رهیافتی مناسب برای نمایش اندازهی یکسان دو مجموعهی بینهایت است.
از آنجایی که تابع f(x) ما تابعی یک به یک و پوشا است، نشان میدهد که دو مجموعهی نامتناهی ℕ و S هم اندازه هستند. حال ممکن است سوال شود که مگر هر عدد طبیعی زوج خودش یک عدد طبیعی نیست و ℕ شامل هر چیزی در S به همراه اعضای خود است، بنابراین آیا ℕ نباید بزرگتر از S باشد؟
در جواب باید گفت که اگر ما با مجموعههای متناهی سر و کار داشتیم، حق با شما بود. اما در مورد یک مجموعهی نامتناهی میتواند بیان کرد که اگر چه یک مجموعهی نامتناهی نوعی، میتواند شامل مجموعه دیگری باشد اما هنوز هم میتواند با آن مجموعه هماندازه باشد. به بیانی دیگر اندازهی مجموعهی بینهایت به اضافهی ۱ با بینهایت برابر است؛ البته این تنها یکی از ویژگیهای شگفتانگیز چنین مجموعههایی است!
در کنار این مشخصهی عجیب می توان مطرح کرد که یکی دیگر از ویژگیهای شگفتانگیز دیگر بینهایتها وجود مجموعههای بینهایت با اندازههای مختلف است! البته لازم به ذکر است که قبلا به این موضوع اشاره کردیم و همانطور که دیدید مجموعههای نامتناهی از اعداد حقیقی و طبیعی طبق اثبات کانتور دارای اندازههای متفاوتی هستند.
مقایسهی بین بینهایتها
از آنجایی که بین هر دو حقیقی و متمایز، بینهایت اعداد حقیقی وجود دارد، اجازه دهید در این قسمت تمرکز خود را روی بینهایت اعداد حقیقی بین صفر و ۱ بگذاریم. همانطور که میدانید هر یک از این اعداد را میتوان به عنوان یک بسط اعشاری (احتمالاً نامتناهی) مانند شکل زیر در نظر گرفت:
در اینجا a1،a2،a3 و بقیه به عنوان ارقام شناخته میشوند و همگی آنها نباید صفر باشند تا عدد صفر نمایش داده نشود. حال طبق اثبات قطری «diagonal argument» اگر بین اعداد طبیعی و این اعداد حقیقی یک تابع یک به یک و پوشا وجود داشته باشد چه اتفاقی میافتد؟ در چنین حالتی، اندازهی دو مجموعه یکسان خواهد بود و میتوان از این تابع برای تناظر هر عدد حقیقی بین صفر و یک، به یک عدد طبیعی استفاده کرد. در این صورت لیستی مرتب شده از تناظر به وجود خواهد آمد که به شرح زیر است:
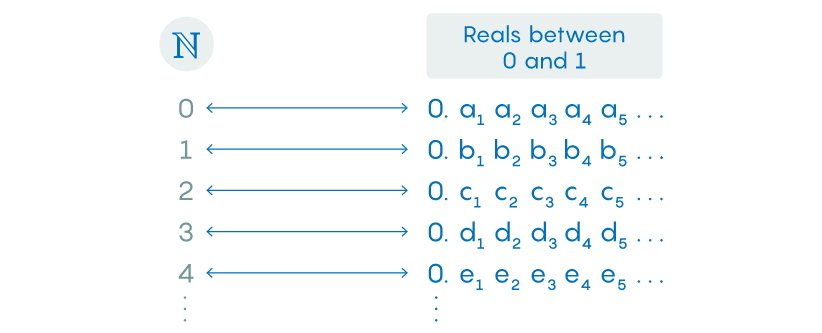
بخش جالبتوجه اثبات قطری این است که میتوان از این لیست برای ساختن یک عدد حقیقی که در لیست نیست، استفاده کرد. به منظور این کار میتوان رویهی زیر را دنبال کرد:
رقم اول بعد از نقطهی اعشار را از a1 متفاوت انتخاب کنید، رقم دوم را از b2 متفاوت کنید، رقم سوم را از c3 متفاوت کنید و به همین شکل ادامه دهید.
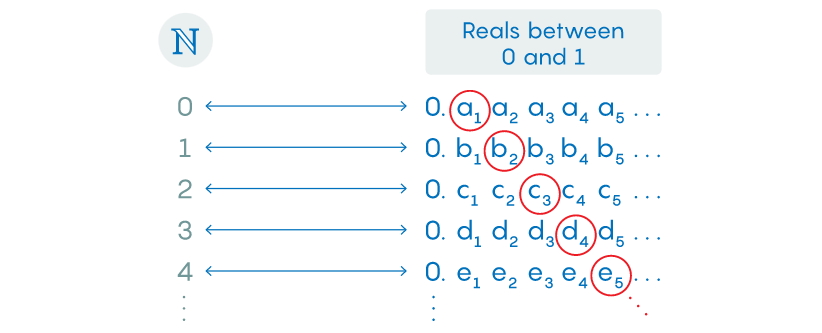
در چنین حالتی عدد حقیقی به واسطهی رابطه با اعداد قطری لیست، تعریف میشود. طبیعتا این عدد حقیقی اولین شماره در لیست نیست چراکه رقم اول لیست متفاوت است. همچنین نمیتواند دومین شمارهی لیست باشد، زیرا رقم دوم هم متفاوت است. این عدد نمیتواند nامین عدد این لیست هم باشد، زیرا رقم nام متفاوتی دارد و این برای همه nهای لیست صادق است، بنابراین این عدد جدید، که بین صفر و ۱ است، در لیست وجود ندارذ.
از طرفی فرض بر این بود که تمام اعداد حقیقی بین صفر تا ۱ در لیست وجود دارند که آشکارا نقض شد. این تناقض از این فرض ناشی میشود که در بین اعداد طبیعی و اعداد حقیقی بین صفر و ۱ یک تابع یک به یک و پوشا وجود دارد ولی فرض نقض شد و مشخص شد که چنین تابعی نمیتواند در لیست وجود داشته باشد. بنابراین این مجموعههای بینهایت، اندازههای مختلفی دارند. با کمی سروکله زدن با توابع میتوان نشان داد که مجموعهی همهی اعداد حقیقی به اندازهی مجموعهی همهی اعداد حقیقی بین صفر و یک است، بنابراین اعداد حقیقیای که شامل اعداد طبیعی میشوند باید مجموعهای بینهایت و بزرگتر باشند. لازم به ذکر است که اصطلاح فنی برای اندازهی یک مجموعهی نامتناهی چیزی به نام کاردینالیتی یا عدد اصلی مجموعه «cardinality» است.
عدد اصلی مجموعه یا کاردینالیتی مجموعهها، یکی از مسائلی است که امکان مرتبسازی مجموعهها را براساس تعداد اعضای آنها فراهم میسازد.
طی همین بررسیها اثبات قطری نشان داد که کاردینالیتهی اعداد حقیقی بیشتر از کاردینالیتهی اعداد طبیعی است. کاردینالیته اعداد طبیعی با ℵ۰ نوشته میشود که «الفا صفر» (aleph naught) تلفظ میشود؛ در یک دیدگاه استاندارد این کوچکترین کاردینال بینهایت است. کاردینال بینهایت بعدی ℵ۱ (آلفا یک) است و پیروی آن سوالی ساده بیان شد که ریاضیدانان را برای بیش از یک قرن درگیر کرد و آن سوال این بود که آیا ℵ۱ کاردینالیتی عددی حقیقی است؟ به عبارت دیگر، آیا بینهایتهای دیگری بین اعداد طبیعی و اعداد حقیقی وجود دارد؟ کانتور فکر میکرد که پاسخ منفی است اما او قادر به اثبات آن نبود. حتی در اوایل دهه ۱۹۰۰، این سؤال به قدری مهم تلقی میشد که وقتی دیوید هیلبرت «David Hilbert» فهرست معروف خود از ۲۳ مسئله مهم و بیپاسخ در ریاضیات را جمع آوری کرد، این بحث مسالهی شمارهی یک او بود. تا اینکه در سال ۱۹۴۰ منطقدان معروفی به نام کورت گودل «Kurt Gödel» ثابت کرد که بر اساس قواعد عمومی پذیرفتهشده در نظریهی مجموعهها، اثبات وجود بینهایتهایی بین اعداد طبیعی و حقیقی غیرممکن است. در آن زمان این موضوع گام بزرگی در جهت اثبات درستی فرضیهی کانتور بود، اما دو دهه بعد، ریاضیدانی به نام پل کوهن «Paul Cohen» نشان داد که اثبات عدم وجود چنین بینهایتی غیرممکن است!
بنابراین گویا ریاضیات با دنیای انتزاعی، ترسناک و شیرین خود هنوز علاقهمند به سرکار گذاشتن ریاضیدانان است.


دیدگاه خود را بنویسید